感知机,Perceptron Learning Algorithm (PLA)

感知机是一种简单非常靠谱的分类算法,首先我们看林老师的PPT：

1571140339242.png

对于$（+1，-1）$的分类，实际上分错分对都是按上述进行更新的。直到没有错误。由向量关系可知，$w$为分类直线的法向量，上图右边表示当$y=+1$时和$y=-1$时，分类直线法向量的更新步骤可以看出：

  • 当$y=+1$分类错误时，$w_t^Tx<0，sign(w_{t+1}^Tx)=-1$,两个向量夹角大于90°，更新后向量夹角小于90°，$w_{t+1}^Tx>0，sign(w_{t+1}^Tx)=+1$，此点更新后分类正确
  • 当$y=-1$分类错误时，$w_t^Tx>0，sign(w_{t+1}^Tx)=+1$,两个向量夹角小于90°，更新后向量夹角大于90°，$w_{t+1}^Tx<0，sign(w_{t+1}^Tx)=-1$，此点更新后分类正确

理论证明：

这里感知机模型为：

变形为:

接着给出式

  • 因为$y(t)\ne \text {sign}(w^T(t)x(t))$，所以当$\text {sign}(w^T(t)x(t))>0 $时，$y(t)=-1$，
    当$\text {sign}(w^T(t)x(t))<0 $时，$y(t)=1$，所以$y(t)w^T(t)x(t) < 0$
  • 如果分类正确则，$y(t)w^T(t)x(t) > 0$

注意$x(t)$的第一个分量为$1$,$w(t)$第一个分量为截距$b$，因为$y^2(t)x^T(t)x(t)>0$，因此

  • 由上我们知道，即使分类错误，$y(t)w^T(t)x(t) < 0$，但利用更新规则后，$y(t)w^T(t+1)x(t)>y(t)w^T(t)x(t)$，也就是向着正方向前进了，即判断的正确率越来越高，所以如果资料是可分的，那么经过有限步之后可以得到$w$，使得对所有的$x$，$yw^Tx>0$

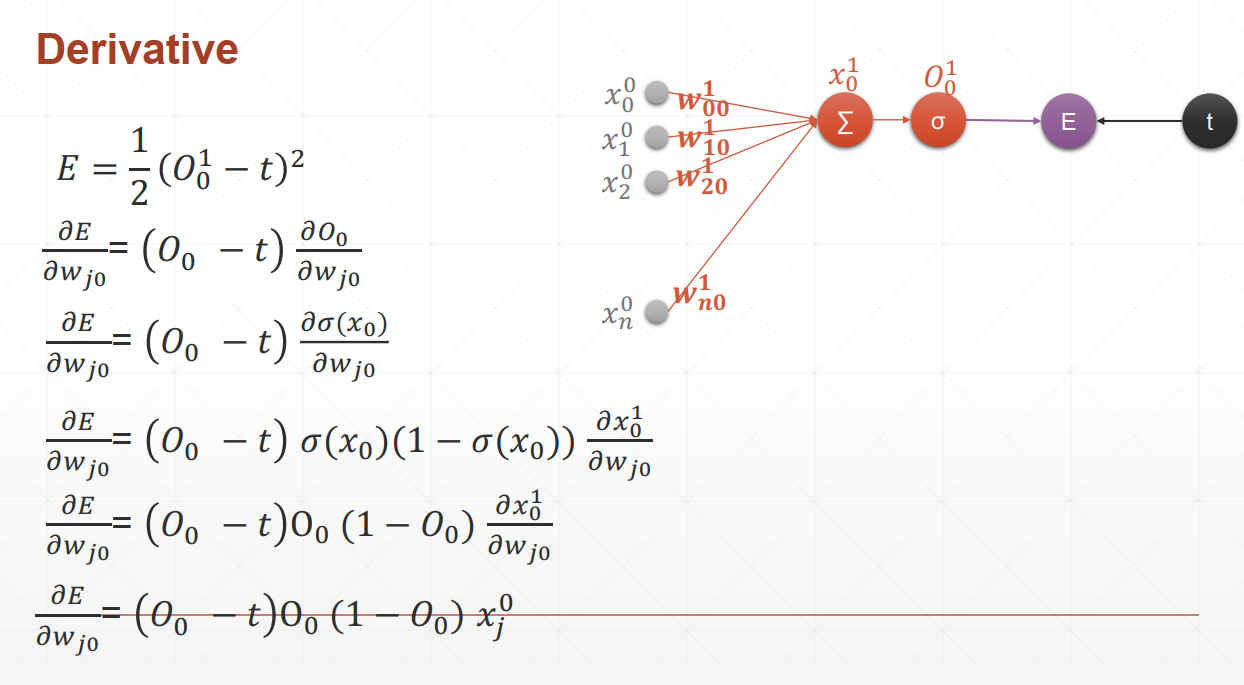
1569464715716.png

编程过程中的图示：

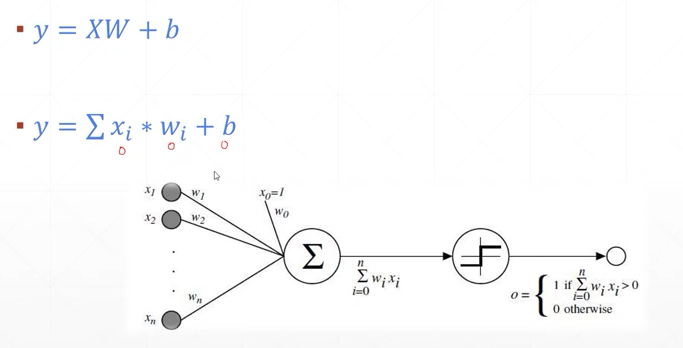
1569464064402.png

由更新规则进行更新，还有就是终止规则：

  • 如果已知线性可分，全部判断对终止。
  • 若是线性不可分，一般设定循环多少次后终止。