[toc]
hash算法及查找
Hash算法是一个广义的算法,也可以认为是一种思想,使用Hash算法可以提高存储空间的利用率,可以提高数据的查询效率,也可以做[字签名来保障数据传递的安全性。所以Hash算法被广泛地应用在互联网应用中。


hash表构造方法:
直接定址法
取关键字或关键字的某个线性函数值为哈希地址。即:H(key)=key 或 H(key) = a * key + b其中a 和 b为常数(这种哈希函数叫做自身函数),

数字分析法
假设关键字是以r为基数的数(如:以10为基的十进制数),并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址(尽量选取不冲突的—重复率少的),也可以在此基础上进行一定的数学处理。

平方取中法
取关键字平方后的中间几位为哈希地址。这是一种较常用的构造哈希函数的方法。通常在选定哈希函数时不一定能知道关键字的全部情况,取其中哪几位也不一定合适,而一个数平方后的中间几位数和数的每一位都有关,由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。
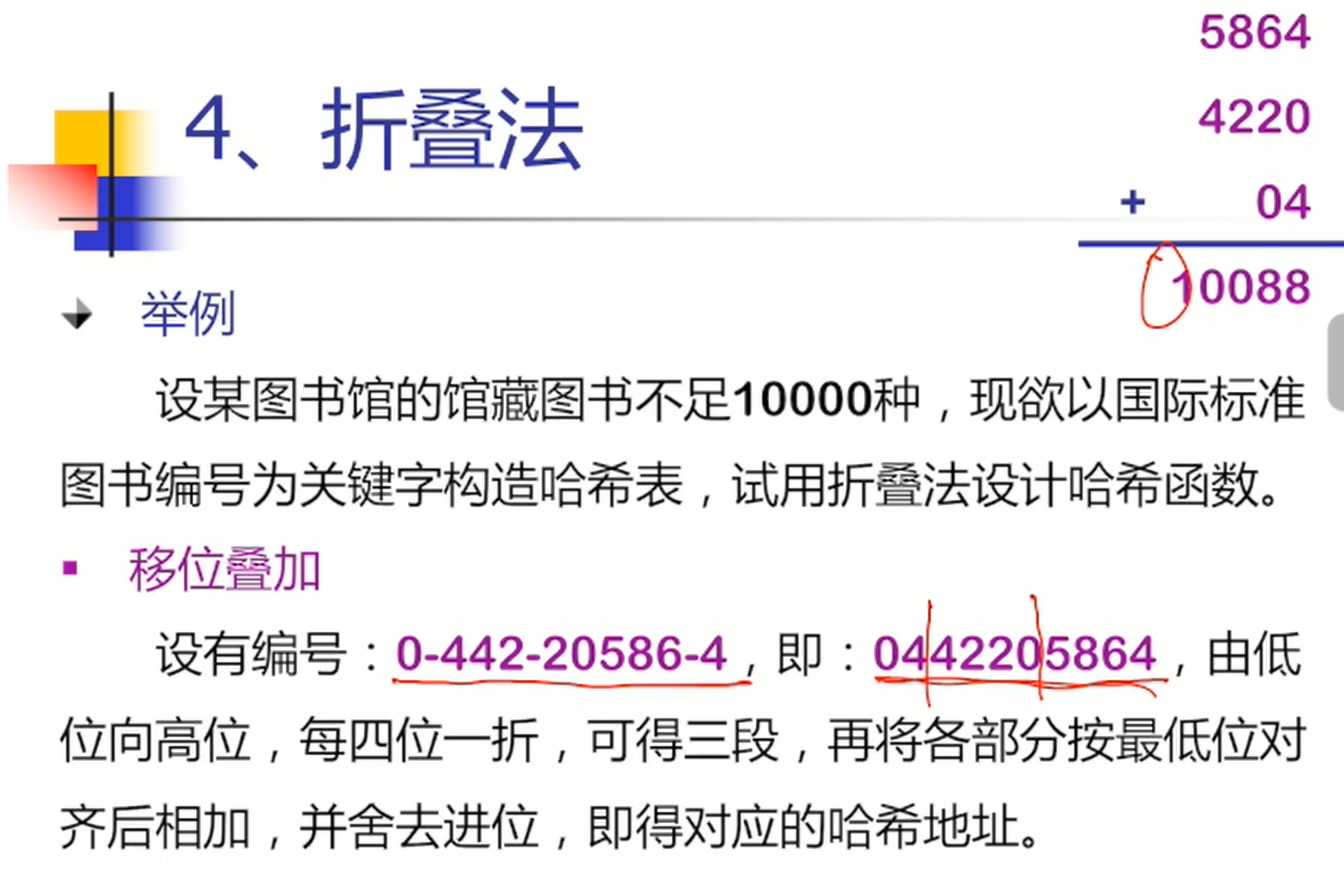
折叠法
将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址,这种方法称为折叠法(folding)。关键字位数很多,而且关键字中每一位数字分布大致均匀时,可以采用折叠法得到哈希地址。


除留余数法
取关键字被某个不大于哈希表表长m的数p除后所得的余数为哈希地址。即
H(key) = key MOD p , p ≤ m 这是一种最简单,也最常用的构造哈希函数的方法。它不仅可以对关键字直接取模(MOD),也可以在折叠、平方取中等运算之后取模。 值得注意的是,在使用除留余数法时,对p的选择很重要。若p选的不好,容易产生同义词。


处理冲突的方法
前面有提到过均匀的哈希函数可以减少冲突,但不能避免,因此,如何处理冲突是哈希造表不可缺少的另一方面。
通常用的处理冲突的方法有下列几种:
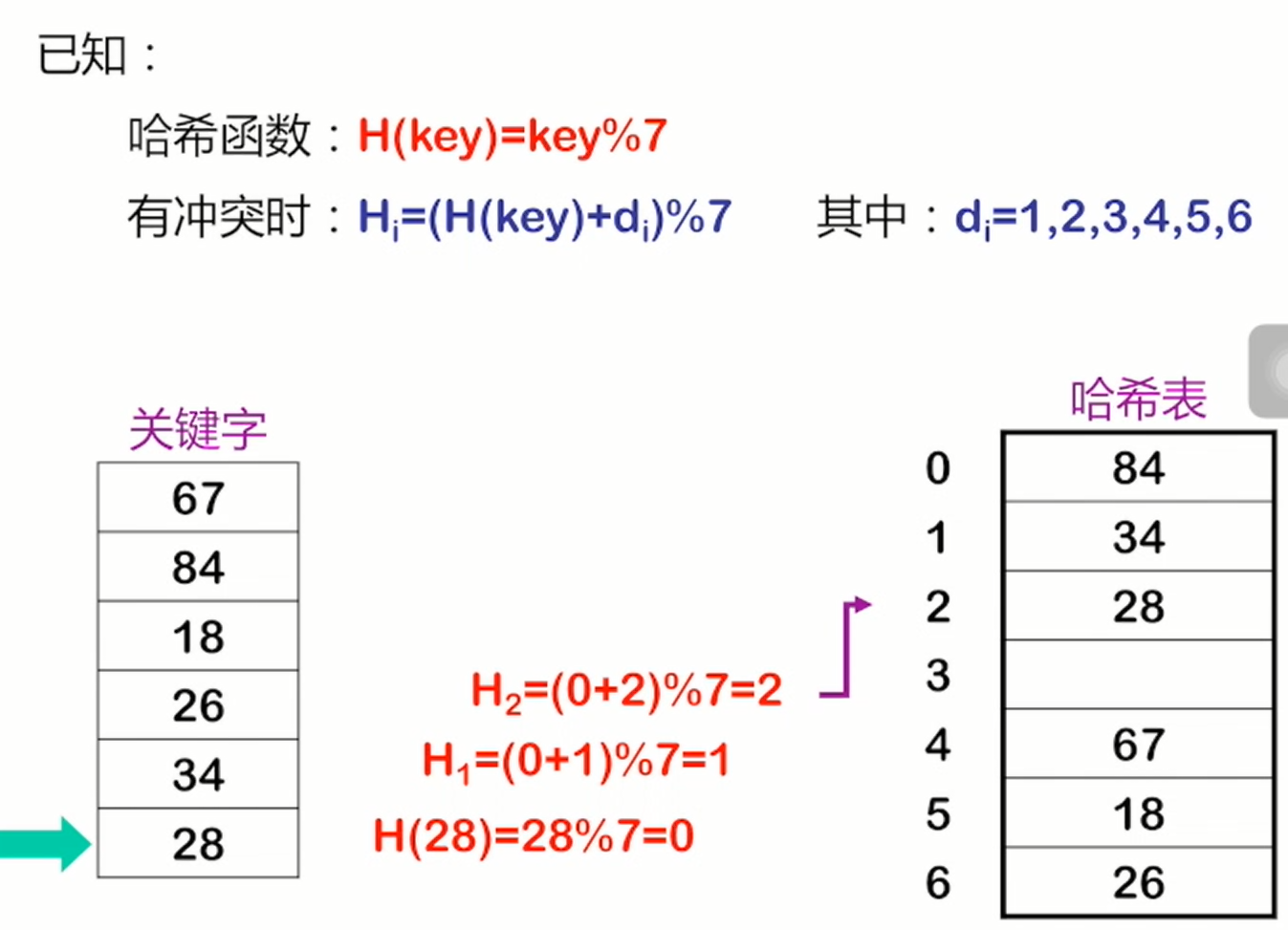
开放定址法



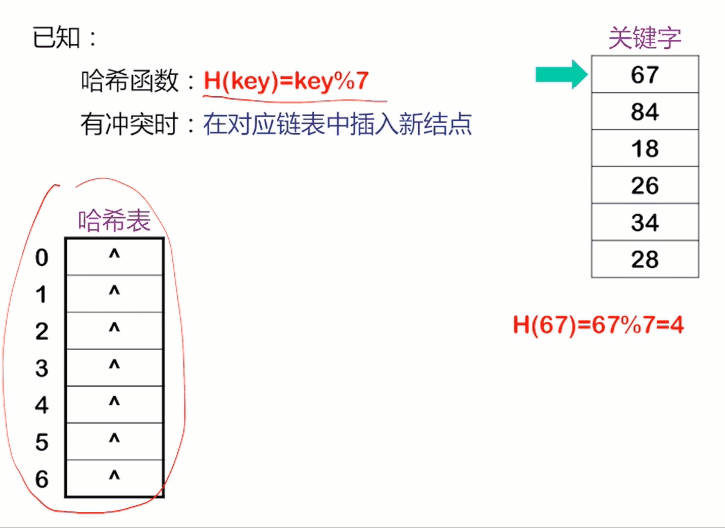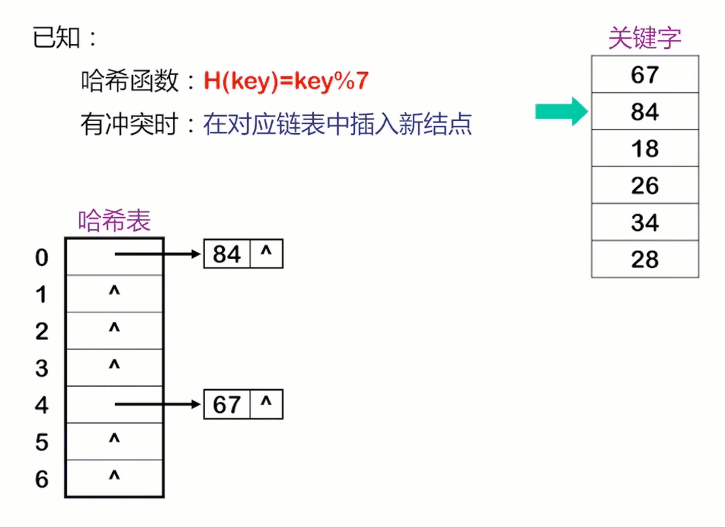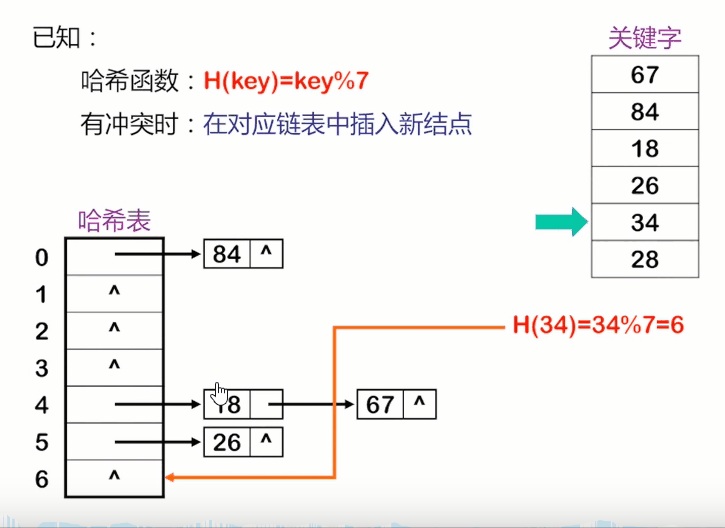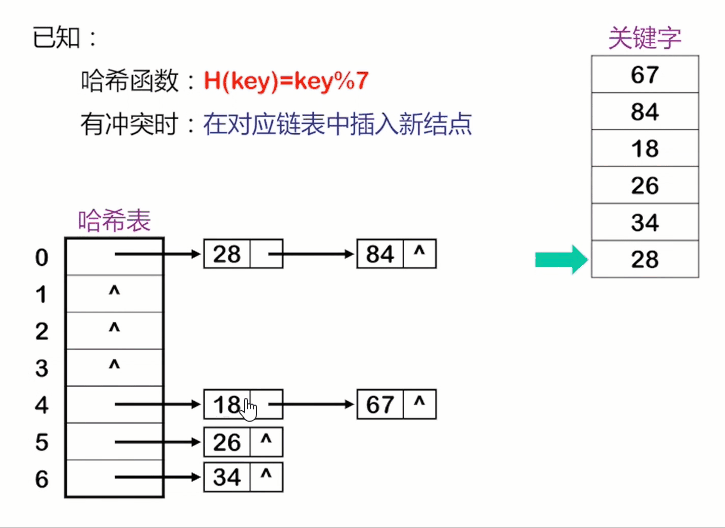
链地址法
将所有关键字为同义词的记录存储在同一线性链表中。假设某哈希函数产生的哈希地址在区间[0,m -1 ]上,则设立一个指针型向量 Chain ChainHash[m] 其每个分量的初始状态都是空指针。凡哈希地址为i的记录都插入到头指针为ChainHash[i]的链表中。在链表中的插入位置可以在表头或表尾;也可以在中间,以保持同义词在同一线性链表中按关键字有序。
建立一个公共溢出区
这也是处理冲突的一种方法、假设哈希函数的值域为[ 0, m - 1 ],则设向量HashTable[ 0..m - 1 ]为基本表,每个分量存放一个记录,另设向量OverTable[0..v]为溢出表。所有关键字和基本表中关键字为同义词的记录,不管它们由哈希函数得到的哈希地址是什么,一旦发生冲突,都填入溢出表。
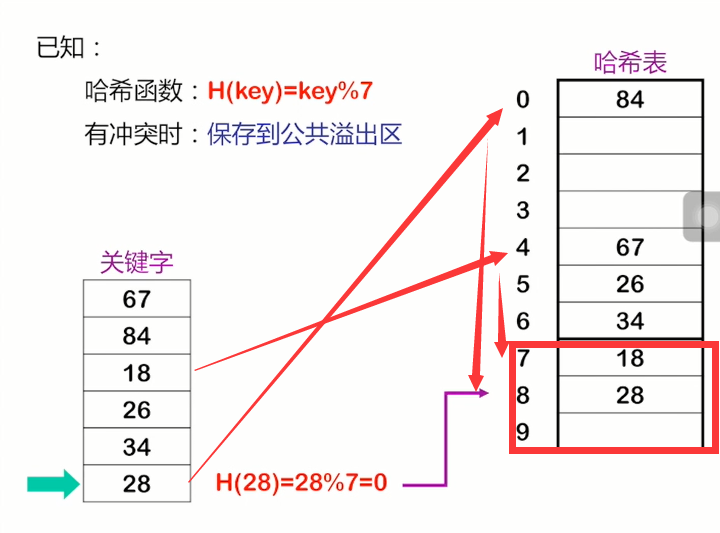
哈希表的查找及其分析
在哈希表上进行查找的过程和哈希建表的过程基本一致。给定K值,根据建表时设定的哈希函数求得哈希地址,若表中此位置上没有记录,则查找不成功;否则比较关键字,若和给定值相等,则查找成功;否则根据造表时设定的处理冲突的方案找“下一地址”,直到找到为止。

参考:
https://www.jianshu.com/p/4cc2cc287e9f

