排序与查找-查找

[TOC]

无序表

  • 如果数据项保存在如列表这样的集合中，我们会称这些数据项具有线性或者顺序关系。
  • 在Python List中， 这些数据项的存储位置称为下标（index） ， 这些下标都是有序的整数。

  • 通过下标， 我们就可以按照顺序来访问和查找数据项， 这种技术称为“顺序查找

  • 要确定列表中是否存在需要查找的数据项

    • 首先从列表的第1个数据项开始，
    • 按照下标增长的顺序，逐个比对数据项，如果到最后一个都未发现要查找的项，那么查找失败 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def sequentialSearch(alist, item):
    pos = 0
    found = False
    
    while pos < len(alist) and not found:
        if alist[pos] == item:
            found = True
        else:
            pos = pos+1

    return found

testlist = [1, 2, 32, 8, 17, 19, 42, 13, 0]
print(sequentialSearch(testlist, 3))
print(sequentialSearch(testlist, 13))

顺序查找的算法复杂度是O(n)

Case Best Case Worst Case Average Case
item is present 1 n n/2
item is not present n n n

顺序查找：有序表

当数据项存在时，比对过程与无序表完全相同不同之处在于，如果数据项不存在，比对可以提前结束 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def orderedSequentialSearch(alist, item):
    pos = 0
    found = False
    stop = False
    while pos < len(alist) and not found and not stop:
        if alist[pos] == item:
            found = True
        else:
            if alist[pos] > item: 
                stop = True # 可以提前终止，因为是有序的
            else:
                pos = pos+1

    return found

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(orderedSequentialSearch(testlist, 3))
print(orderedSequentialSearch(testlist, 13))

顺序查找有序表的各种情况分析

Case Best Case Worst Case Average Case
item is present 1 n n/2
item is not present 1 n n/2
  • 实际上， 就算法复杂度而言， 仍然是O(n)
  • 只是在数据项不存在的时候， 有序表的查找能节省一些比对次数， 但并不改变其数量级

二分查找

从列表中间开始比对
如果列表中间的项匹配查找项，则查找结束
如果不匹配，那么就有两种情况：

  • 列表中间项比查找项大，那么查找项只可能出现在前半部分
  • 列表中间项比查找项小，那么查找项只可能出现在后半部分
    • 无论如何，我们都会将比对范围缩小到原来的一半： n/2
    • 继续采用上面的方法查找，每次都会将比对范围缩小一半 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
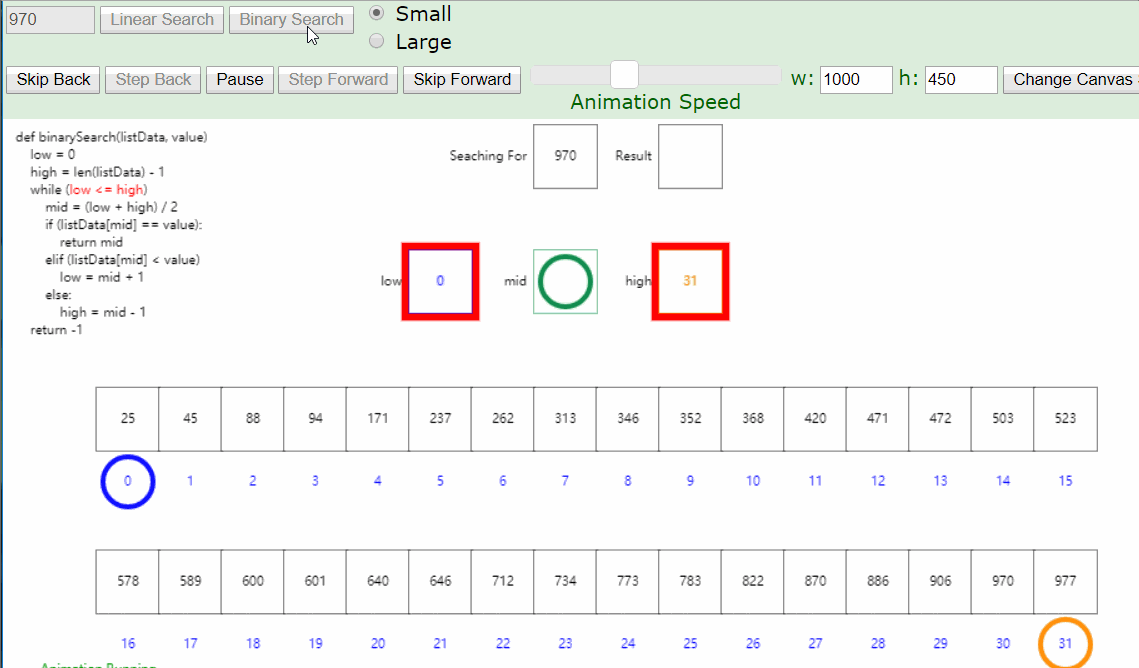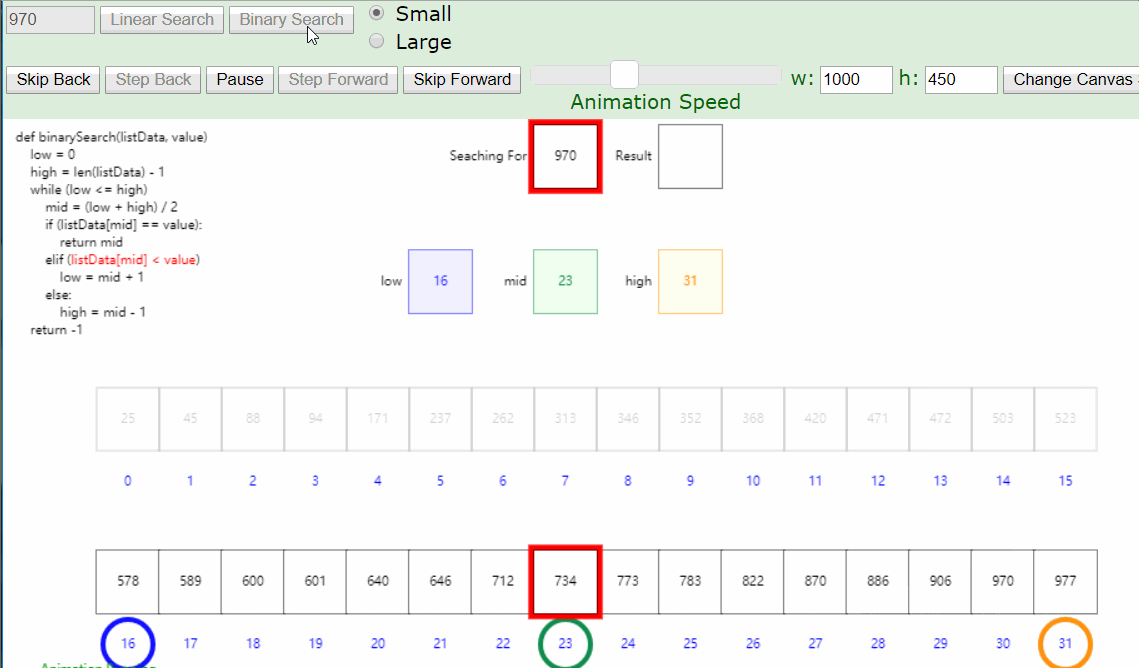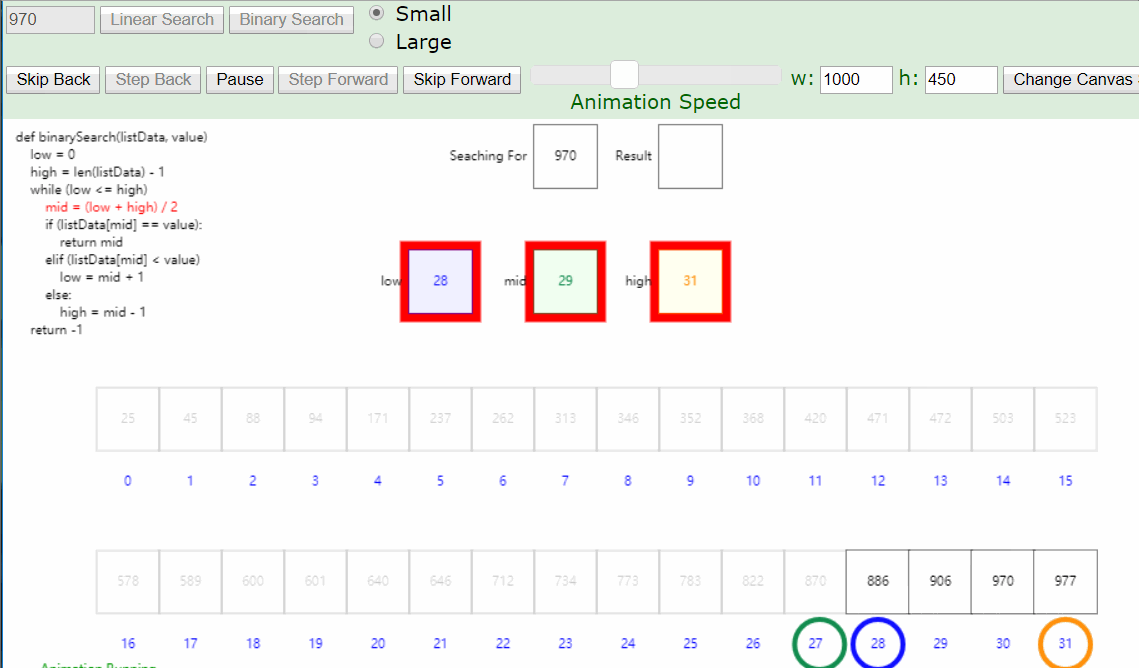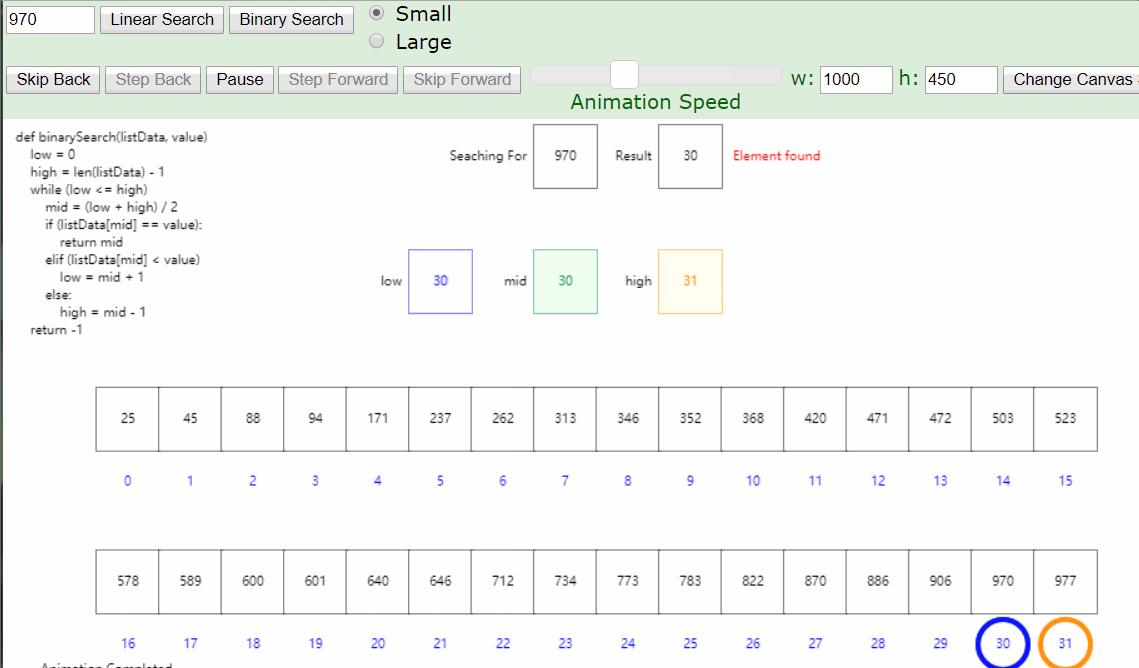
20
def binarySearch(alist, item):
    first = 0
    last = len(alist)-1
    found = False

    while first<=last and not found:
        midpoint = (first + last)//2
        if alist[midpoint] == item:
            found = True
        else:
            if item < alist[midpoint]:
                last = midpoint-1
            else:
                first = midpoint+1

    return found

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 13))

分而治之

二分查找算法实际上体现了解决问题的典型策略： 分而治之，将问题分为若干更小规模的部分，通过解决每一个小规模部分问题，并将结果汇总，得到原问题的解

二分查找 - 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def binarySearch(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
        if alist[midpoint]==item:
          return True
        else:
          if item<alist[midpoint]:
            return binarySearch(alist[:midpoint],item)
          else:
            return binarySearch(alist[midpoint+1:],item)

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 13))

由于二分查找， 每次比对都将下一步的比对范围缩小一半，每次比对后剩余数据项如下表所示：

Comparisons Approximate Number of Items Left
1 n/2
2 n/4
3 n/8
…
i $n/2^i$

当比对次数足够多以后， 比对范围内就会仅剩余1个数据项,二分法查找的算法复杂度是O(log n)

  • 虽然我们根据比对的次数， 得出二分查找的复杂度O(log n)

  • 但本算法中除了比对， 还有一个因素需要
    注意到：

    • binarySearch(alist[:midpoint],item)这个递归调用使用了列表切片，而切片操作的复
      杂度是O(k)，这样会使整个算法的时间复杂度稍有增加；
    • 当然，我们采用切片是为了程序可读性更好，实际上也可以不切片，而只是传入起始和结束的索引值即可，这样就不会有切片的时间开销了。

  • 另外， 虽然二分查找在时间复杂度上优于顺序查找

  • 但也要考虑到对数据项进行排序的开销

    • 如果一次排序后可以进行多次查找，那么排序的开销就可以摊薄
    • 但如果数据集经常变动，查找次数相对较少，那么可能还是直接用无序表加上顺序查找来得经济

  • 所以， 在算法选择的问题上， 光看时间复杂度的优劣是不够的， 还需要考虑到实际应用的情况。